Purpose: To investigate the conditions for rotational equilibrium of a rigid bar and to determine the center of gravity of a system of masses.
Equipment: Meter stick, meter stick clamps (knife edge clamp), balance support, mass set, weight hangers,
unknown masses, balance.
Introduction: The condition for rotational equilibrium is that the net torque on an object about some point in the body, O, is zero. Remember that the torque is defined as the force times the lever arm of the force with respect to the chosen point O. The lever arm is the perpendicular distance from O to the line of action of the force.
mass A of 171.4g @ .285m from 0
mass B of 121.3 g @ .404m from 0
The masses of the clamps must be included in the calculations because they are part of the mass that affects the balance of the system.
Torque(T) = Force x lever arm
Force is mass a of gravity / Lever = distance from 0
Tnet = Ta -Tb = 0
(0.1714kg)(9.8m/s^2090.285m) - (0.1213kg)(9.8m/s^2)(0.404m) = 0
0.478720-0.480251= 0.001531
As we can see this number is not quite 0
% diffrence = (theoretical -experimental/ theoretical) x 100
% diffrence is (0.285911m - 0.285 m/ (0.285911m) x 100 = 0.32 %
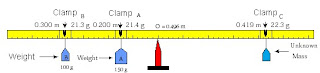
Third we got the same two masses used above and placed them at different locations on the same side of the support and balance the system with a third mass on the opposite side. Our three masses where
mass A of 171.4g @ .200m form 0
mass B of 121.3 @ 0.300m form 0
mass C of 272.3 @ 0.261m form 0
Tnet = Ta + Tb - Tc = 0
0.335944 +0.356622 -0.696489 = -0.003923
as we can see agin our number doesnt add up to 0
% difference = (0.259530 - 0.261/ 0.259530) x 100 = 0.57 %
Next we replaced one of the above masses with an unknown mass. Readjusting the position of the masses we were able to achieve equilibrium at
Mass A 171.4 @ .0200m from 0
mass B 121.3 @ 0.300m form 0
mas unknown @ 0.419m for 0
T net = Ta+ Tb - Tu = 0
0.335944+0.356622) + mass U kg x 4.106 m/s ^2 = 0.168663 kg - Clamp = 0.146363 kg
Unknown mass wighed at 0.1469kg using the balance
That gives a pecent diffrence of .37 %
For our next experiment we placed 200 grams at 90 cm mark on the meter stick and balance the system getting a new center of balance. From this info we calculated the mass of the meter stick
position of new 0 on meter stick = .762m
position previous 0 on metestick = .496m
Distance of the 200g mass from the new 0 = 0.138m
Distance of the previous 0 to thenew 0 = 0.266m
Tnet=T 200 - Tr = 0
Calculated mass of ruler 0.103759kg
Ruler weighted @ 0.1032 kg using the balance
% difference = .54 %
It is not necessary to include the mass of the clamp holding the ruler in the calculations because it is at the fulcrum, it doesn't affect the balance.
Last we imagined that we positojn an additonal 100g mass at the 30 cm mark on teh meter stick. Calculating the positon of the center of gravity of this combo gave us
T100+ Tr = T 200
Tr = 0.200kg
0 new = 0.261187 kg / 0.4032 kg = 0.647785m
@ experiment its 0.646m
% diffrence = (0.646-0.647785)/ (0.646) x 100 = .28 %
Conclusion: This lab was one with the least percent error. In all of our calculations we were getting less an 1 percent. We all agreed that there is little room for error in this lab since it wont take much for the ruler to tip to a side. But yet there were some % error. This was probably do to the fact that at times the ruler wouldn't balance stright. It would rest at a slight angle. We also talked about the inconsestency of the wood being a factor for % error but over all we able to get some very good results with this lab. I cant imagine doing a lab like this with out the use of our new friend, Torque. Thanks to our torque formulas we were able to investige the conditons for rotational equilibrium of a rigid bar and determine the center of gravity of a system of masses.
No comments:
Post a Comment